Y x-3 graph linear inequalities 272233-How do you graph a linear inequality

Linear equations can be written in the form;One way to visualize twovariable inequalities is to plot them on a coordinate plane Here is what the inequality x > y looks like The solution is a region, which is shaded There are a few things to notice here First, look at the dashed red boundary line this is the graph of the related linear equation x = y Next, look at the light redHow to graph linear inequalities how to graph systems of linear inequalities We also have a systems of inequalities calculator that can display the shaded region that satisfies all the given inequalities Graphing Linear Inequalities In the following diagram, all the points above the line y = 1 are represented by the inequality y > 1

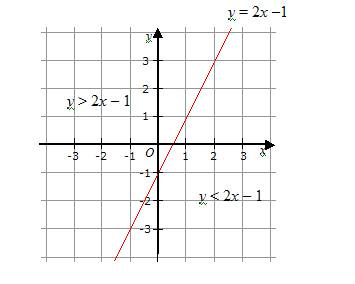
Which Is The Graph Of The Linear Inequality Y X 3 Brainly Com

How do you graph a linear inequality

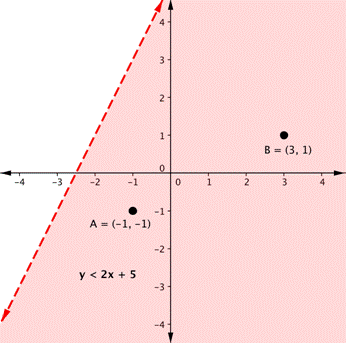
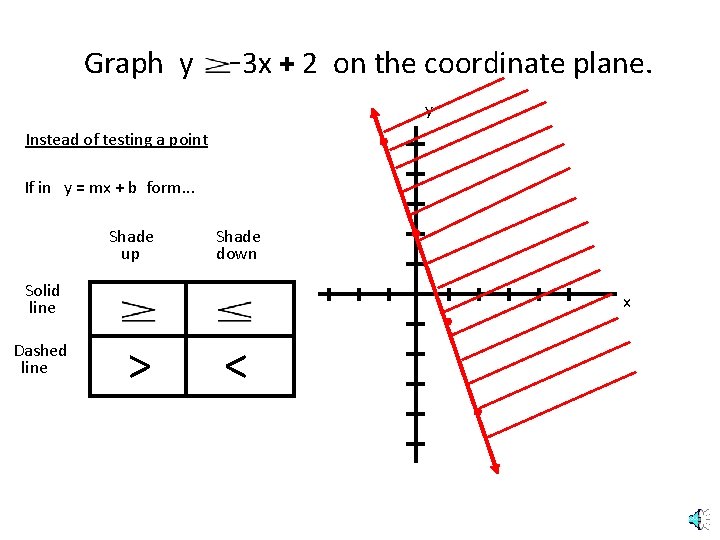
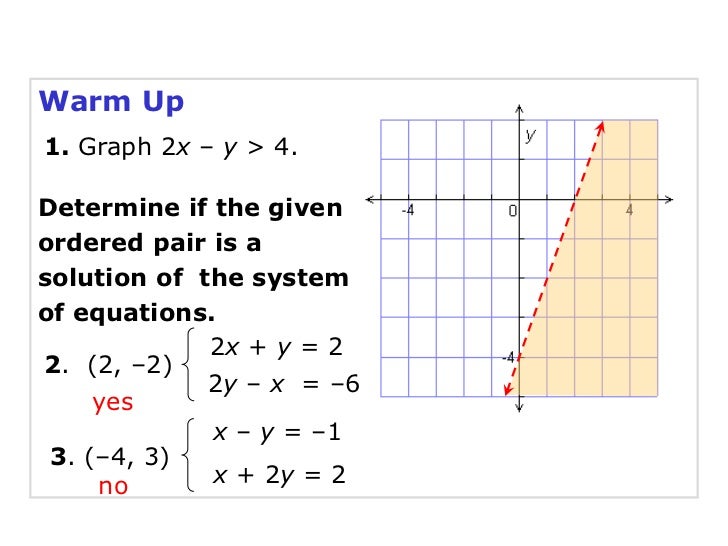
How do you graph a linear inequality-Section 31 Graphing Systems of Linear Inequalities in Two Variables Procedure for Graphing Linear Inequalities 1 Draw the graph of the equation obtained for the given inequality by replacing the inequality sign with an equal sign Use a dashed line if the problem involves a strict inequality, < or >Write the inequality of the graph shown Ex Ex Find equation of the line by finding m and b m = 1, b = –3 so y = x – 3 Inequality sign is > or < since line is dotted Origin does not work Plug in (0, 0) and choose y < –2x 3 inequality sign that makes it false y < x – 3

6 4 Linear Inequalities And Systems Of Linear Inequalities In Two Variables Hunter College Math101

Solving and graphing linear inequalities Transcript Created by Sal Khan and Monterey Institute for Technology and Education Google Classroom Facebook Twitter Email Onestep inequalities Onestep inequalities examples Onestep inequalities 5c ≤ 15 Onestep inequalityD Which linear inequality is represented by the graph?Graph one inequality First graph the boundary line, then test points Remember, because the inequality 3 x 2 y < 12 3 x 2 y < 12 does not include the equal sign, draw a dashed border line Testing a point like ( 0, 0) ( 0, 0) will show that the area below the line is the solution to this inequality

Which is the graph of the linear inequality 2x 3y < 12?How to Graph a Linear Inequality First, graph the "equals" line, then shade in the correct area Rearrange the equation so "y" is on the left and everything else on the right Plot the " y= " line (make it a solid line for y≤ or y≥, and a dashed line for y< or y>) or below the line for a "less than" ( y< or yA The solutions to the inequality y > −3x 2 are shaded on the graph Which point is a solution?

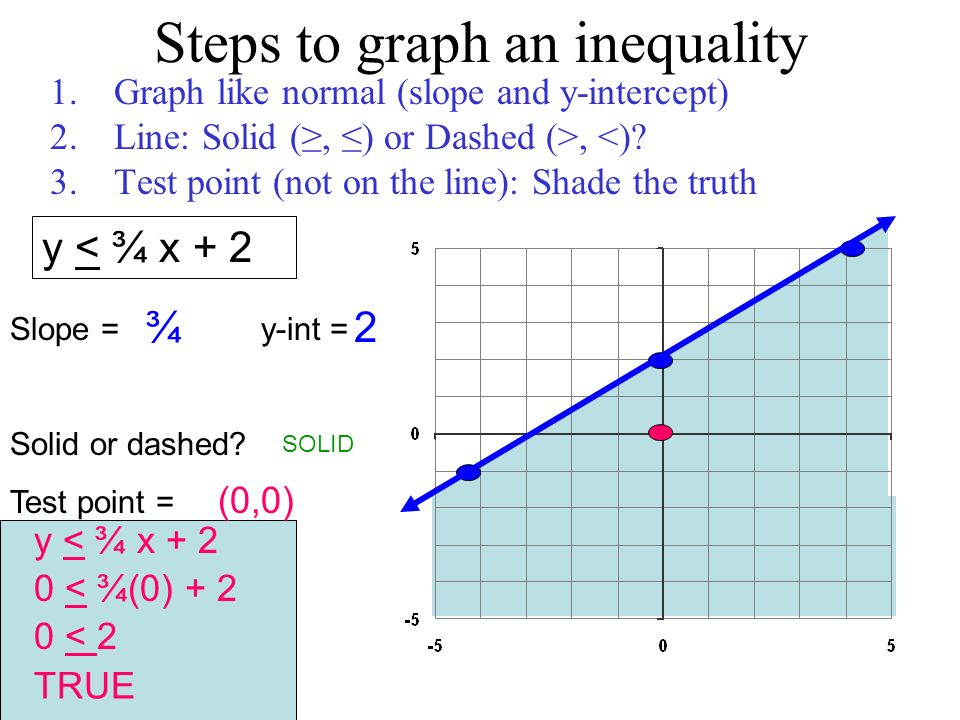
28 – Graph Linear Inequalities in Two Variables Example 8 Graph y > 2x – 3 4 28 – Graph Linear Inequalities in Two Variables A linear inequality in two variables can be written in one of these forms Ax By < C Ax By < C Ax By > C Ax By > C An ordered pair (x, y) is a solution of a linear inequality in two variables if the 23K answers 71M people helped It's te 1st graph Why?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

1

Graphing Linear Inequalities Kate S Math Lessons

Graphing Linear Inequalities Lesson Steps to graphing inequalities 1 Rewrite inequality in slopeintercept form 2 Determine whether to use a solid or a dashed line 3 Determine whether to shade above or below the line Example Graph the following inequalities a) 2x 4y ≥ 16 b) y 1 < 2x c) y ≥ 1/2 x 3 d) 5x 3y > 9 e) y < 4 It is easier to work with straight lines in the form y = mx c In this case y < x 3 One can choose xvalues, work out yvalues and plot points, or, use the slope and intercept method This line crosses the yaxis at 3 and has a gradient of 1 (ie it is at 45° from top left to bottom right, cutting the yaxis at 3) However, as this is an inequality with only a "less than" 1 We will need to rearrange this one so "y" is on its own on the left Start with 2y − x ≤ 6 Add x to both sides 2y ≤ x 6 Divide all by 2 y ≤ x/2 3 2 Now plot y = x/2 3 (as a solid line because y≤ includes equal to) Graphing Linear Inequalities

Section 6 5 Linear Inequalities Is The Ordered Pair A Solution For Y X 3 A 1 2 How Do We Know If 1 2 Is A Solution Y X 3 Ppt Download

4 1 Graphing Linear Inequalities In Two Variables Mathematics Libretexts

 Which graph shows the solution to the system of linear inequalities?5 4 3 2 1 x o vex 3 and 3x – y> 2 o vax 3 and 3x=y=2 Oy2 x3 and 3x y> 2 O yax 3 and 2x – 1= 2 eeduanswerscomGraphing linear inequalities in two variables and find common region In this section, we will learn, how to graph linear inequalities and find the solution using the common region in graph To obtain the common region for both the given linear inequalities, we have to follow the steps given below

Graphing Inequalities Solutions Examples Videos

Graphing Linear Inequalities

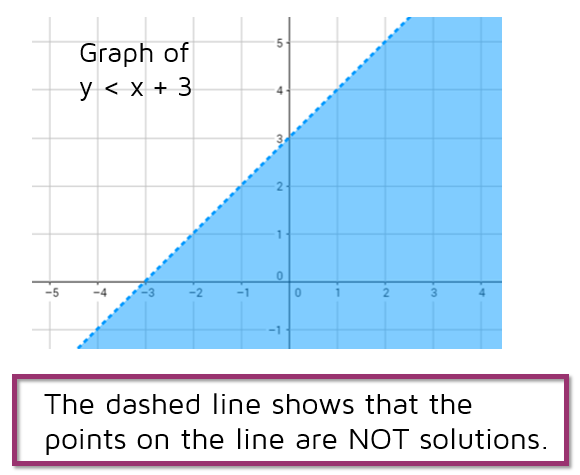
Students learn to graph inequalities in two variables For example, to graph y x 2, the first step is to graph the boundary line y = x 2, using the chart method from lesson 4BNote that greater than or less than means that the boundary line will be dotted, and greater than or equal to or less than or equal to means that the boundary line will be solidSolution Step 1 First graph 2x y = 4 Since the line graph for 2x y = 4 does not go through the origin (0,0), check that point in the linear inequality Step 2 Step 3 Since the point (0,0) is not in the solution set, the halfplane containing (0,0) is not A linear inequality is an inequality that can be written in one of the following forms A x B y > C A x B y ≥ C A x B y < C A x B y ≤ C Where A and B are not both zero Recall that an inequality with one variable had many solutions For example, the solution to the inequality x>3x>3 is any number greater than 3

Solving Inequalities With Two Variables

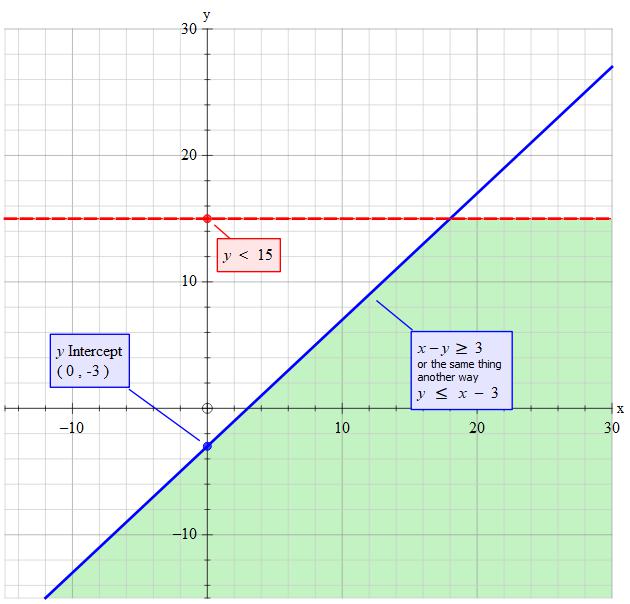
How Do You Graph The System Of Linear Inequalities X Y 3 And Y 15 Socratic

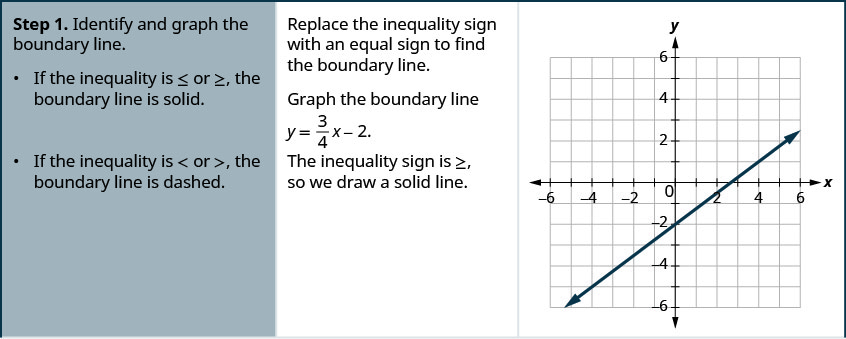
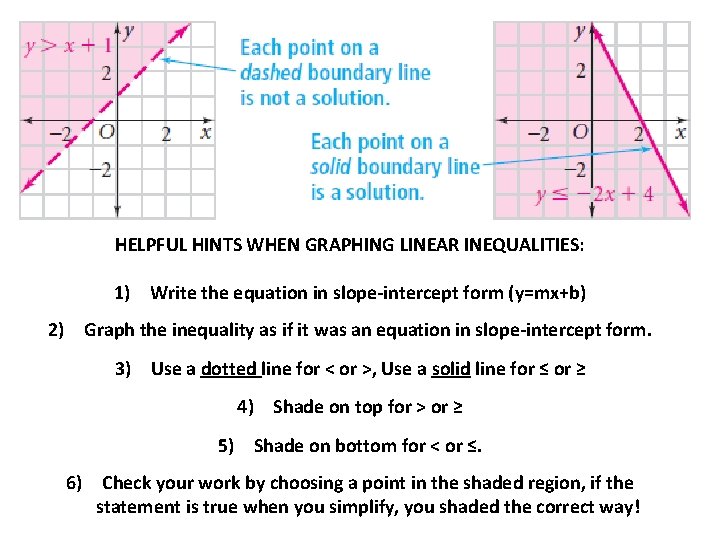
 👍 Correct answer to the question Which system of linear inequalities is represented by the graph?Section 1 Graphing Using the Rectangular Coordinate System Select Section 31 Graphing Using the Rectangular Coordinate System 32 Graphing Linear Equations 33 Intercepts 34 Slope and Rate of Change 35 Slope–Intercept Form 36 Point–Slope Form 37 Graphing Linear Inequalities 38 An Introduction to Functions 0029 Graph the linear inequality The steps we take to graph a linear inequality are summarized here Graph a linear inequality Identify and graph the boundary line If the inequality is , the boundary line is solid If the inequality is < or >, the boundary line is dashed Test a point that is not on the boundary line

Graphing Systems Of Linear Inequalities Ck 12 Foundation

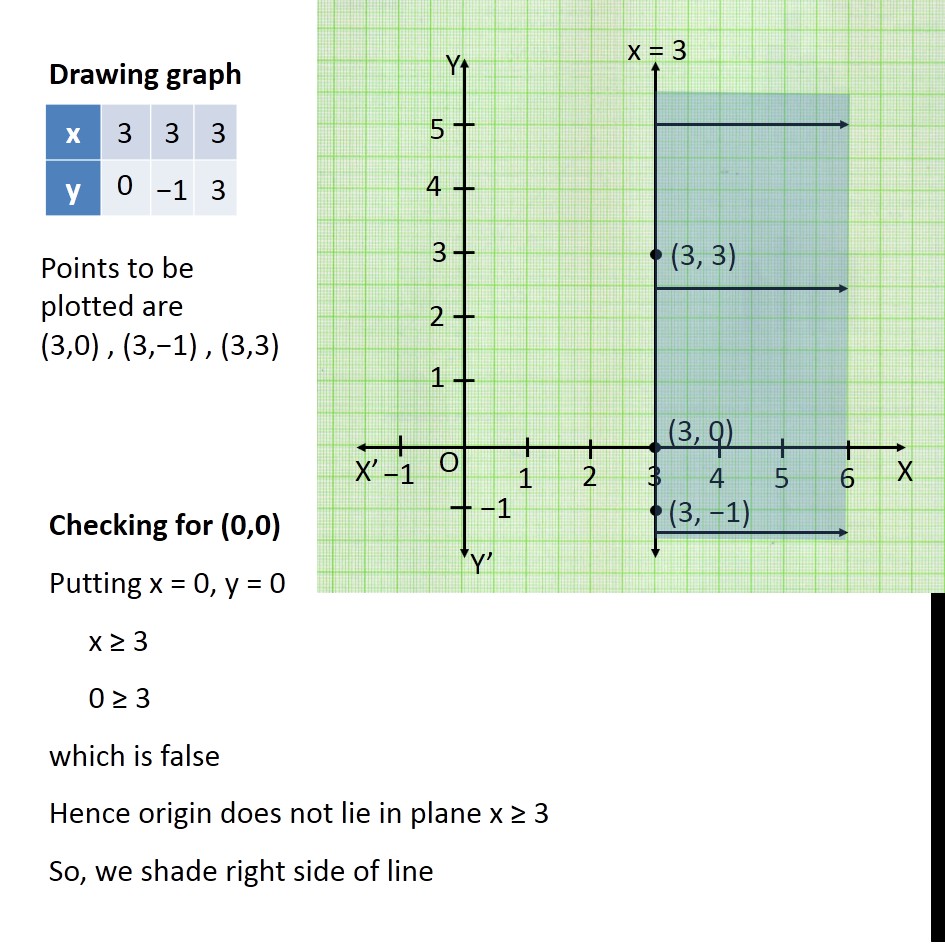
Ex 6 3 1 Solve X 3 Y 2 Graphically Chapter 6 Ncert

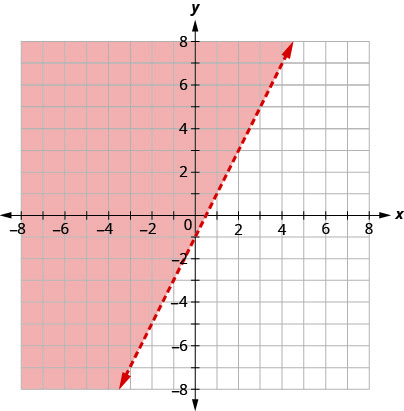
Those two activities can give you practice in drawing graphs of linear inequalities in Mobius Part a Find two points on the associated line Often it's smart to start with the values x = 0 and x = 1 The point (0, ) is on the line y=4x3 The point (1, ) is on the line y=4x3 Part b Find a point that satisfies the strict inequality y>4x3NOT (0, 2) (2, 0) Which is the graph of the linear inequality 1/2x 2y > 6?The inequality is y ≥ −x − 3, it means could be EQUAL OR Greater than x3 Then the line is consistent, where the 3rd graph shows that the line is dotted, that mean it's ONLY greater & can't be equal taffy927x2 and 266 more users found this answer helpful

3 8 Linear Inequalities Two Variables Mathematics Libretexts

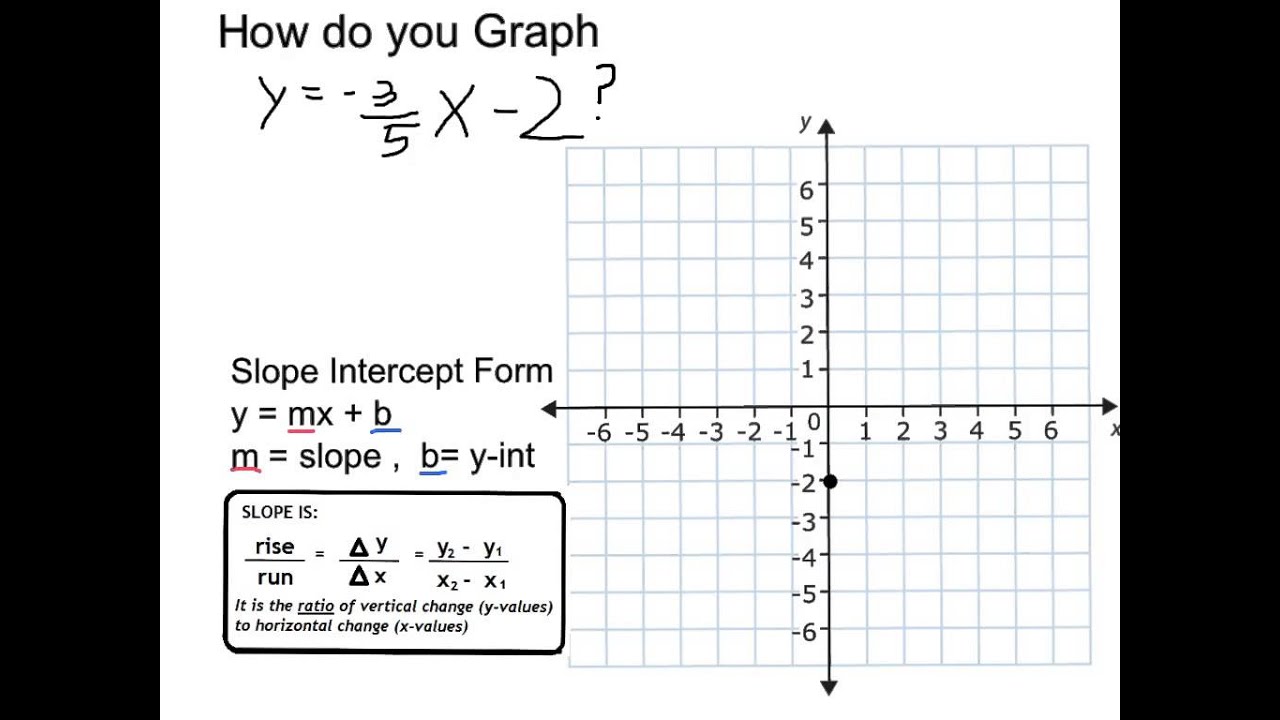
Graph Y 3 5 X 2 Youtube

Free System of Inequalities calculator Graph system of inequalities and find intersections stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicySolve linear inequalities, stepbystep \square!👉 Learn how to graph linear inequalities written in slopeintercept form Linear inequalities are graphed the same way as linear equations, the only differe

Ex 6 3 10 Solve 3x 4y 60 X 3y 30 X 0 Y 0

Solving Linear Inequalities Objectives To Graph And Solve

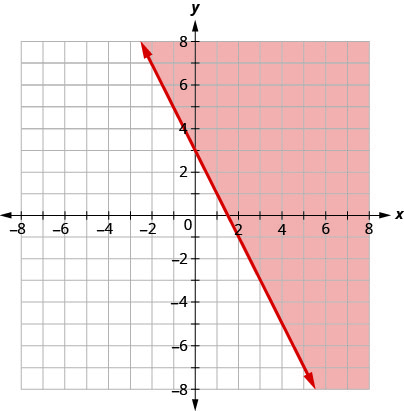
Which is the graph of the linear inequality y ≥ −x − 3?Graph 6x 3y – 4z = 12 The xintercept is where the plane passes through the xaxis, and so y = 0 and z = 0 6x 3(0) – 4(0) = 12 6x = 12 x = 2 Then we find the yintercept 6(0) 3y – 4(0) = 12 3y = 12 y = 4 And finally the zintercept 6(0) 3(0) – 4z = 124z = 12 z = 3 The intercepts are (2, 0, 0), (0, 4, 0), and (0, 0, 3) Connect them up inside the graphing cube Here are the steps to graphing a linear inequality 1 Rearrange the Linear Inequality Similar to a Linear Equation First, rearrange the linear inequality so that the yvariable is on one side This is very similar to if you were graphing the line by itself You want the equation of the line to be in a y = mx b format

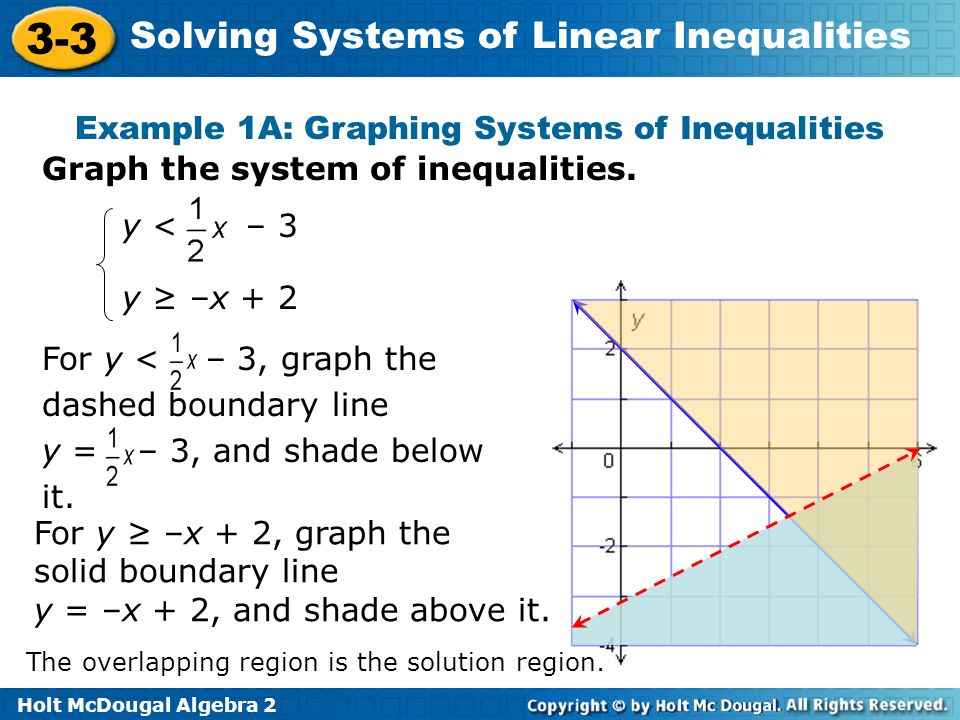
3 3 Solving Systems Of Linear Inequalities Warm Up Lesson Presentation Ppt Video Online Download

Inequalities Graphing Inequalities Sparknotes

 y = 1 or (4,1) We can now graph the two points on the coordinate plane and draw a line through the points to mark the boundary of the inequality graph { (x^2 (y3)^035) ( (x4)^2 (y1)^035) (yx3)=0 10, 10, 5, 5} Now, we can shade the right side of the line We also need to change the boundary line to a dashed line because theGraphing Systems of Linear Inequalities To graph a linear inequality in two variables (say, x and y ), first get y alone on one side Then consider the related equation obtained by changing the inequality sign to an equality sign The graph of this equation is a line If the inequality is strict ( < or > ), graph a dashed lineGraph of a system of linear inequalities Core Concepts Graphing a System of Linear Inequalities Step 1 Graph each inequality in the same coordinate plane Step 2 Find the intersection of the halfplanes that are solutions of the inequalities This intersection is the graph of the system Inequality 2 Notes y x x y 4 6 2 4 y < x 2 y ≥ 2x − 1

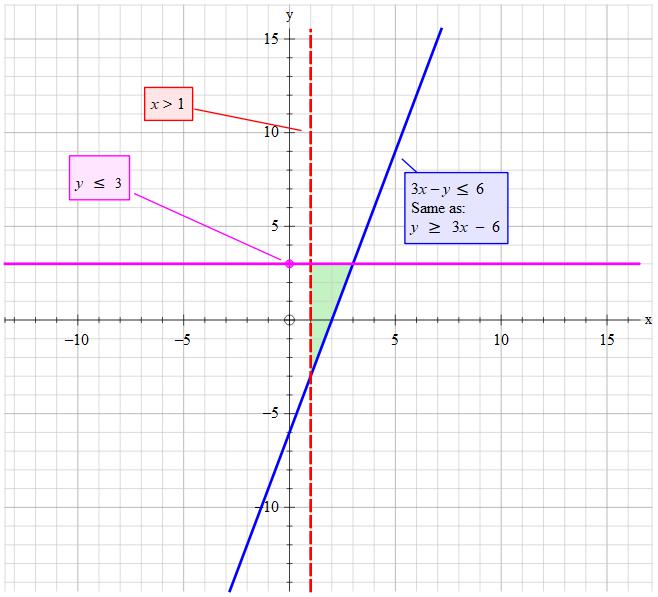
How Do You Graph The Inequality 3x Y 6 X 1 And Y 3 Socratic

Graphing Linear Inequalities Chilimath

X – 4y 4 y x 1 On a coordinate plane, 2 straight lines are shown The first solid line has a positive slope and goes through (0, negative 1) and (4, 0) Everything above the line is shaded The second dashed line has a positive slope and goes through (negative 1, 0) and (0Have students create a chart that compares and contrasts graphing an inequality in one variable with graphing an inequality in two variables To help concrete learners, use graph paper to keep the information linear Enlarge the copies of the pieces of the Solving Inequalities Puzzle to make the problems more distinctC Graph Three (dashed line shaded above) The solutions to the inequality y ≤ 2x − 4 are shaded on the graph

How Do You Graph The Inequality Y 3 Socratic

Linear Inequalities And Systems Of Linear Inequalities In Two Variables Math Modeling

Graph a linear inequality Identify and graph the boundary line If the inequality is \(\le \text{or}\ge \), the boundary line is solid If the inequality is < or >, the boundary line is dashed Test a point that is not on the boundary line Is it a solution of the inequality? Exercise 477 The boundary line shown is 2x 3y = 6 Write the inequality shown by the graph Answer The line 2 x 3 y = 6 is the boundary line On one side of the line are the points with 2 x 3 y > 6 and on the other side of the line are the points with 2 x 3 y < 6Answer to Graph the solution of the system linear inequalities y \geq x 3 \\y \geq 5 x By signing up, you'll get thousands of stepbystep

Linear Inequalities How To Graph The Equation Of A Linear Inequality

Graphing Linear Inequalities

Unit 4 Systems of Equations and Inequalities Lesson 23 Graphing Linear Inequalities 509 9 3x" 6 10 3 & y!Step by step guide to graphing linear inequalities First, graph the "equals" line Choose a testing point (it can be any point on both sides of the line) Put the value of (x,y) ( x, y) of that point in the inequality If that works, that part of the line is the solution If the values don't work, then the other part of the line is the3 ' 0 12 Open Ended Create 5 ordered pairs using the whole digits 0—9 exactly one time each Then create a linear inequality such that M Two of the ordered pairs are solutions to the linear inequality

Graphing Linear Inequalities In Two Variables Lesson Essential

Section 7 5 Graphing Linear Inequalities Objectives To

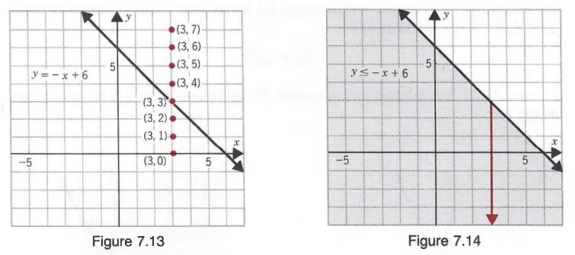
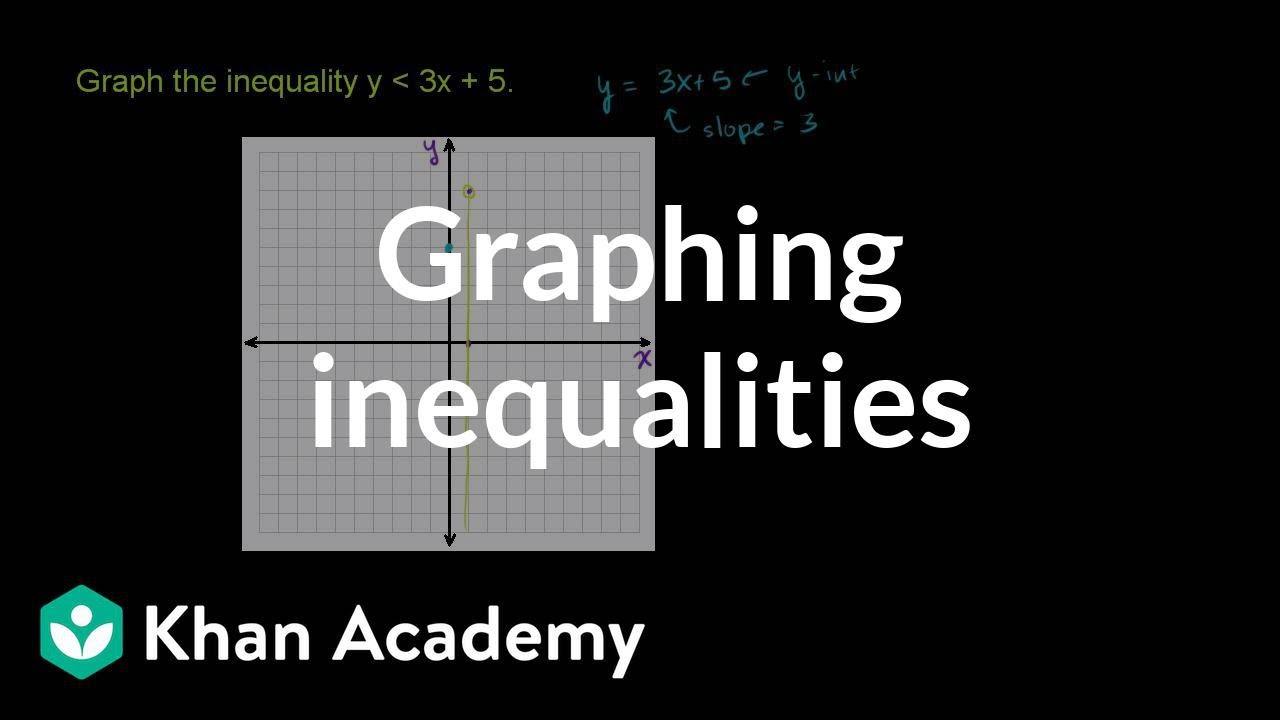
In this case, that means the "equals" part is the line y👉 Learn how to graph linear inequalities written in standard form Linear inequalities are graphed the same way as linear equations, the only difference beiThe steps for graphing twovariable linear inequalities are very much the same Graph the solution to y < 2 x 3 Just as for numberline inequalities, my first step is to find the "equals" part For twovariable linear inequalities, the "equals" part is the graph of the straight line;

How Do You Graph Y X 2 Color White D Y 3x 2 Socratic

E9zc0qhlevm2sm

Graph y ≥ 2 x 3 First, graph y = 2 x 3 (see Figure 3) Notice that the boundary is a solid line, because the original inequality is ≥ Now, select a point not on the boundary, say (2,1), and substitute its x and y values into y ≥ 2 x 3 This is not a true statementX y 8) x y 9) y 10) x y 11) x y 12) x y Critical thinking questions 13) Name one particular solution to # 14) Can you write a linear inequality whose solution contains only points with positive xvaluesHowever, liner inequalities come in several different forms These forms include Graphing such inequalities differs a little from graphing regular equations Graphing the line in an inequality doesn't change from the original process, but how the line appears on the graph does change

4 1 Graphing Linear Inequalities In Two Variables Mathematics Libretexts

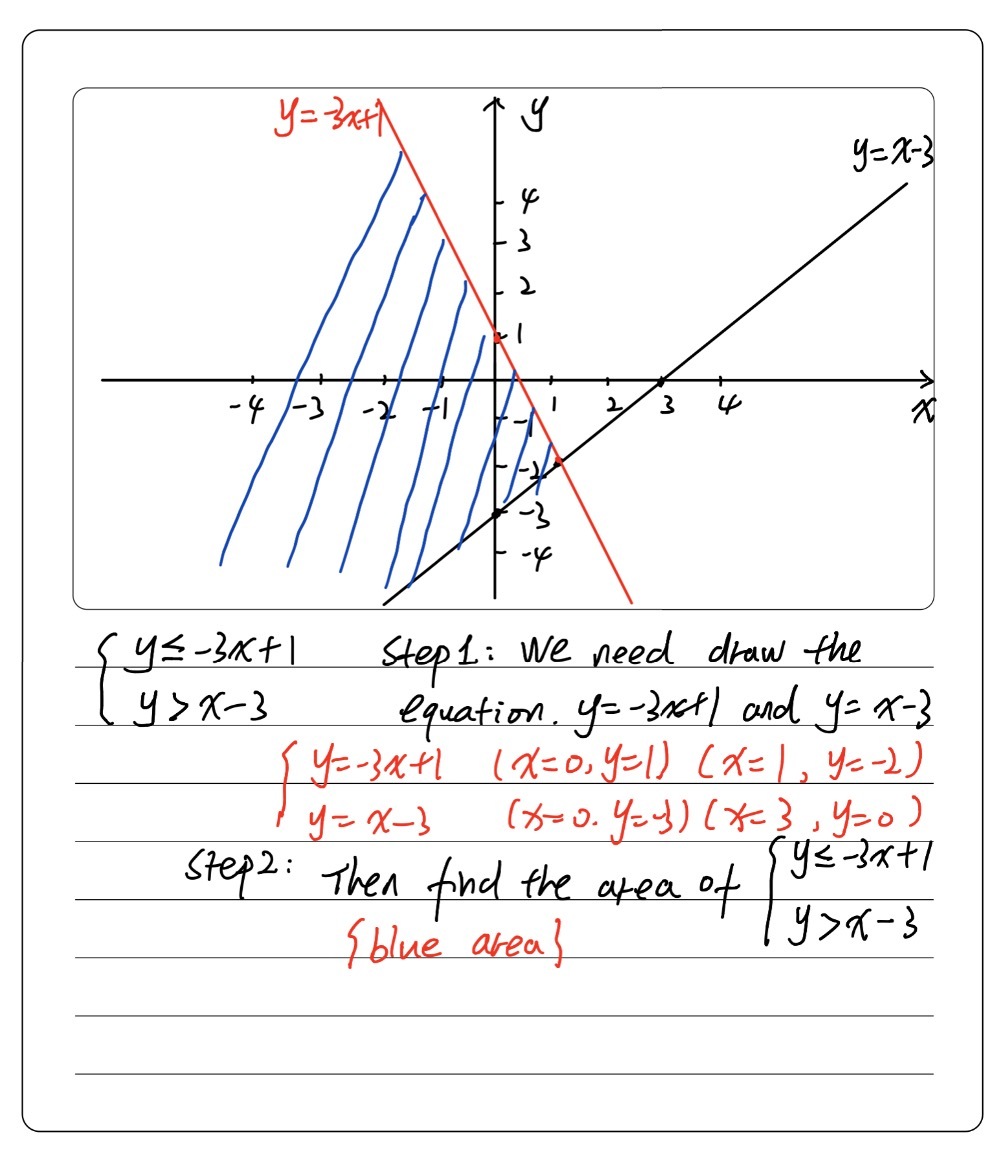
Graph The System Of Linear Inequalities Y 3 Gauthmath

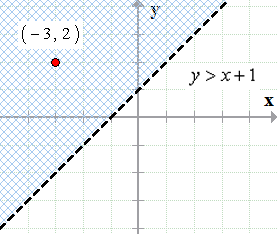
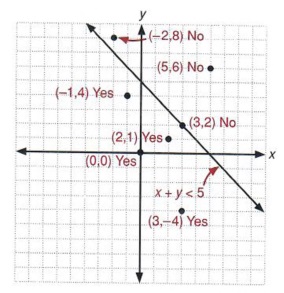
 Linear inequalities are the expressions where any two values are compared by the inequality symbols such as, '', '≤' or '≥' These values could be numerical or algebraic or a combination of both For example, 1017 are examples of numerical inequalities and x>y, y 11 are the examples of algebraicBelow is the graph of the inequality y > x 1 Step 1 The inequality is already in the form that we want That is, the variable y is isolated on the left side of the inequality Step 2 Change inequality to equality Therefore, y > x 1 becomes y = x 1 Step 3 Now graph the y = x 1Use the method that you prefer when graphing a lineNow, we will look at how the solutions of an inequality relate to its graph Let's think about the number line in Figure 430 again The point x = 3 x = 3 separated that number line into two parts On one side of 3 are all the numbers less than 3 On the

Which System Of Linear Inequalities Is Represented By The Graph Y Gt X 3 And 3x Y Gt 2 Y Brainly Com

Which Is The Graph Of The Linear Inequality Y X 3 Brainly Com

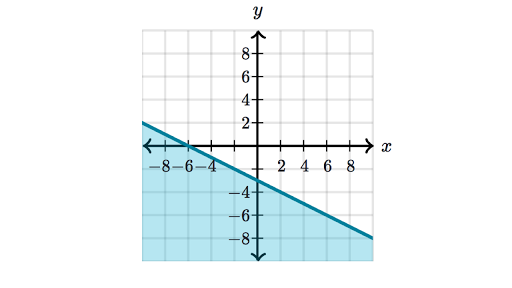
Graphing Inequalities X Y Plane Review Article Khan Academy

Graphing Linear Inequalities

Linear Inequalities Two Variables

Which Is The Graph Of The Linear Inequality Y X 3 Brainly Com

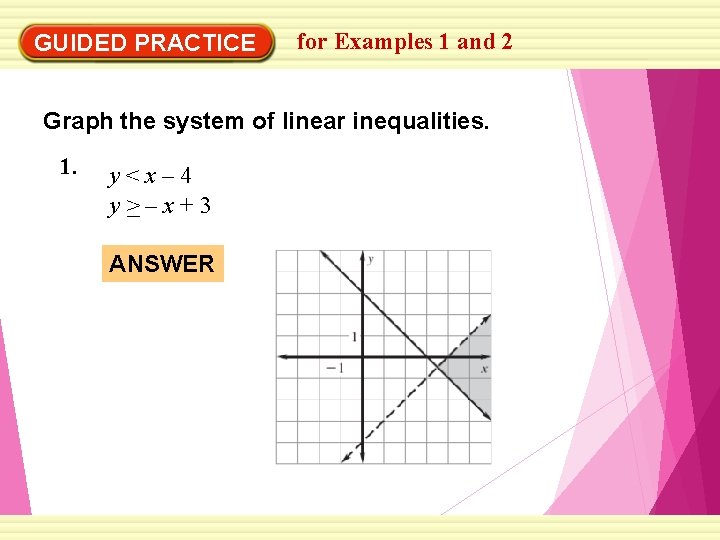
7 6 Solve Systems Of Linear Inequalities Example

Graph Inequality On Coordinate Plane Youtube

Graphing Inequalities X Y Plane Review Article Khan Academy

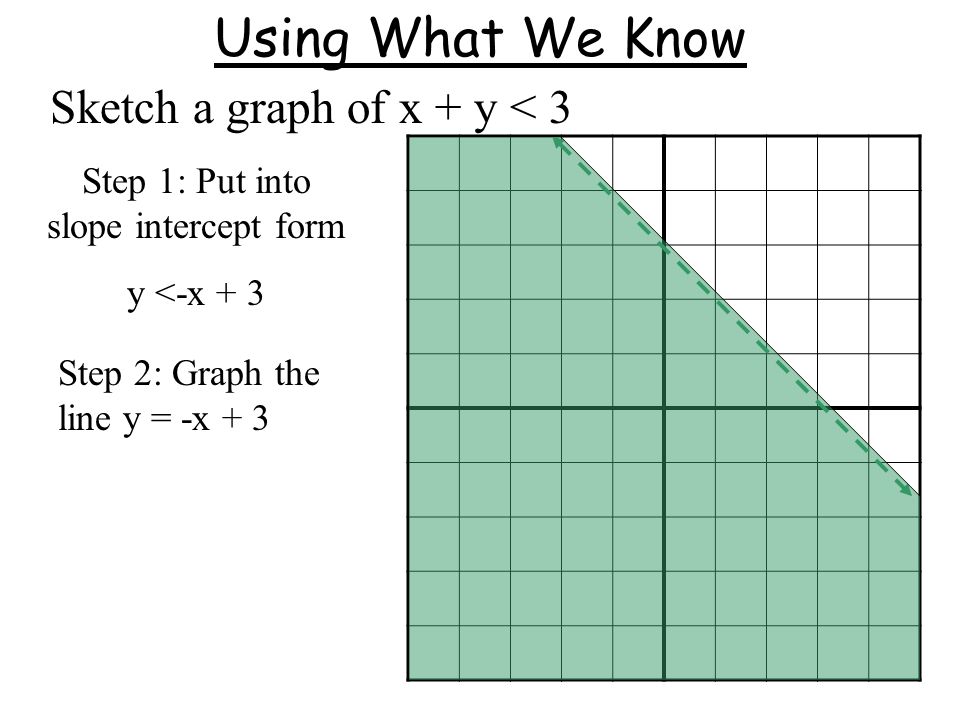
Graphing Linear Inequalities In Two Variables Swbat Graph A Linear Inequality In Two Variables Swbat Model A Real Life Situation With A Linear Inequality Ppt Download

Graphs And Solutions To Systems Of Linear Equations Beginning Algebra

Graphing Linear Inequalities

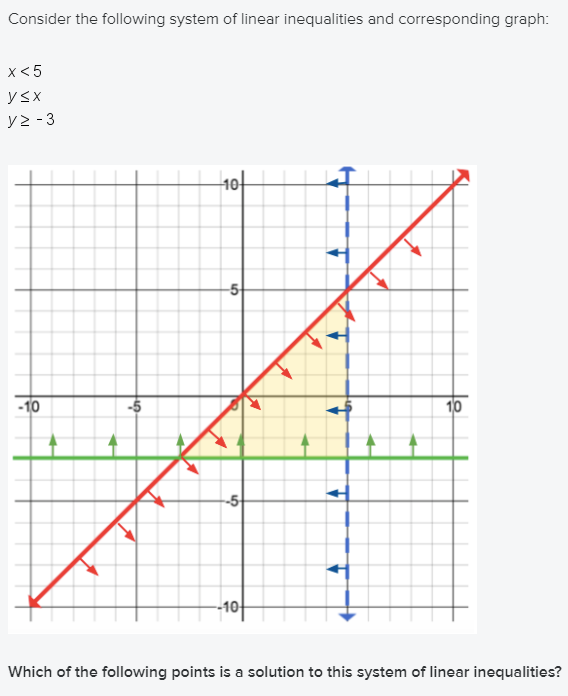
Consider The Following System Of Linear Inequalities Chegg Com

Linear Programming Read Algebra Ck 12 Foundation

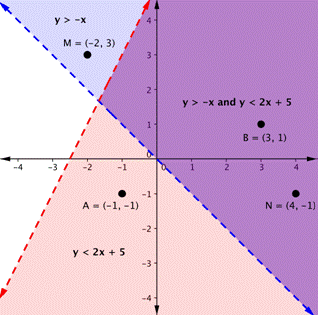
6 4 Linear Inequalities And Systems Of Linear Inequalities In Two Variables Hunter College Math101

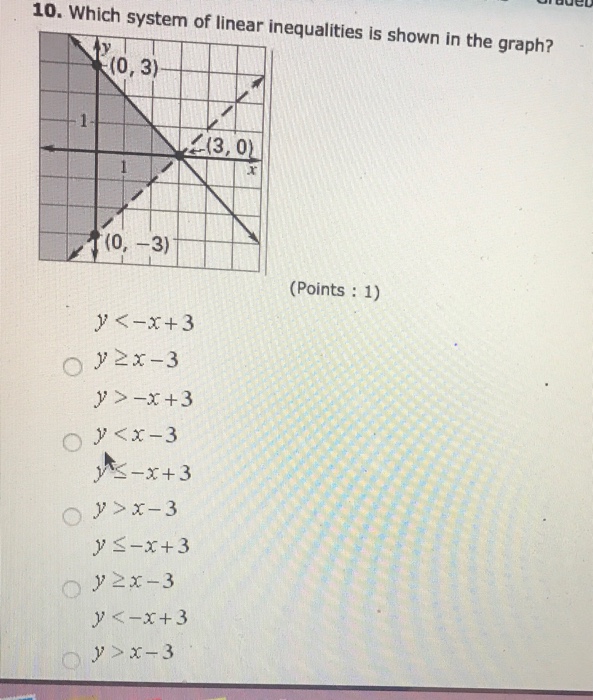
Which System Of Linear Inequalities Is Shown In The Chegg Com

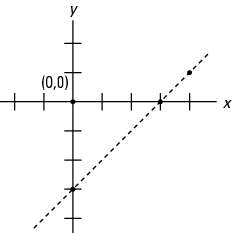
Linear Inequalities And Half Planes

Graph Graph Equations With Step By Step Math Problem Solver

Graphing Two Variable Inequalities Video Khan Academy

Graphing Linear Inequalities Expii

Graphing Linear Inequalities In Two Variables And Find Common Region

Graphing Linear Inequalities

Solving Systems Of Linear Inequalities Two Variables

Ex 6 3 11 Solve 2x Y 4 X Y 3 2x 3y 6

Ex 6 3 12 Solve Graphically X 2y 3 3x 4y 12

Objectives Learn To Solve Linear Inequalities 3x 2y 6 Y 0 Ppt Download

How Do You Graph The Solution Of The System Of Linear Inequalities X 3y And X 2y 10 Homeworklib

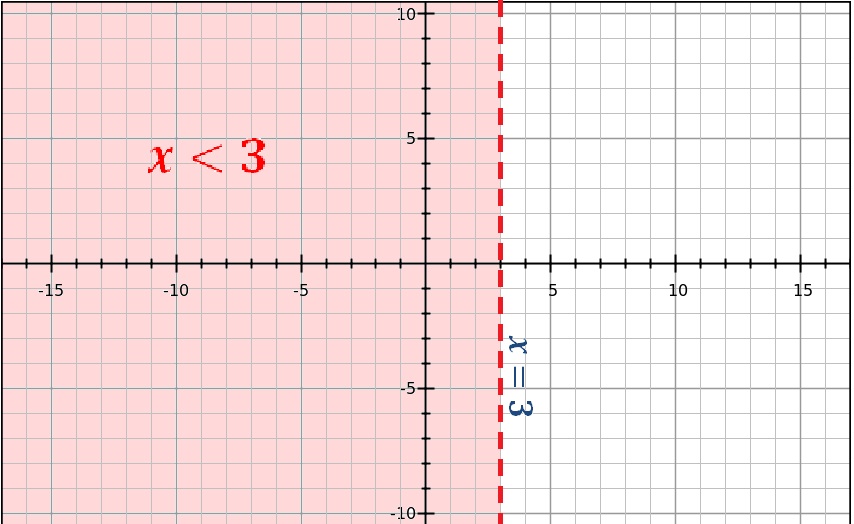
How Do You Graph The Inequality X 3 Socratic

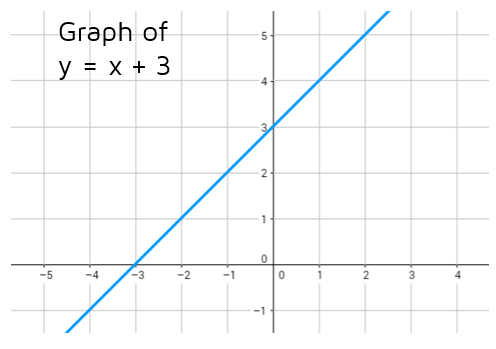
Graphing Linear Inequalities Kate S Math Lessons

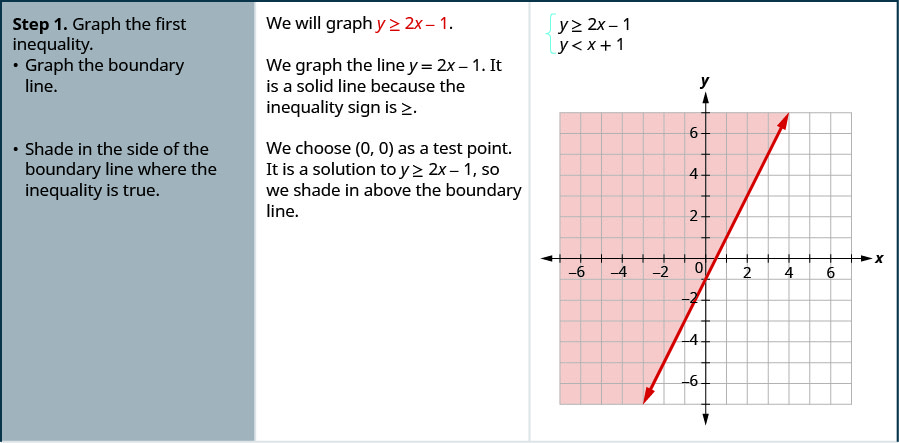
4 2 Graphing Systems Of Linear Inequalities Mathematics Libretexts

7 5 Linear Inequalities Objective

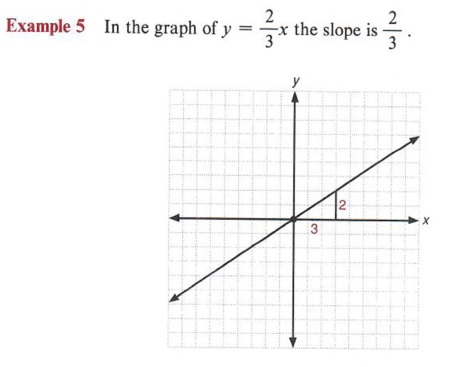
Graph Graph Inequalities With Step By Step Math Problem Solver

Solve The Following System Of Inequalities Graphically 4x 3y 2x X 3 X X 0

Graph Graph Inequalities With Step By Step Math Problem Solver

Linear Inequalities How To Graph The Equation Of A Linear Inequality

Linear Inequalities Alg 1 P 6 Ochs 14 15

Linear Inequalities In Two Variables Algebra 1 Linear Inequalitites Mathplanet

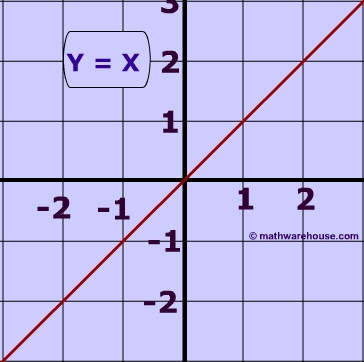
How To Graph The Line Y X Youtube

4 1 Graphing Linear Inequalities In Two Variables Mathematics Libretexts

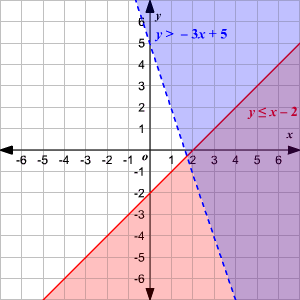
Graphing Systems Of Linear Inequalities

Linear Inequalities How To Graph The Equation Of A Linear Inequality

Solution Graph The System Of Linear Inequalities X Lt 3 2x Y Gt 7 There Is Suppose To Be A Under The Lt Sign By The 3 Please Explain To Me How You Get The Points To

Linear Inequalities Notes

Ixl Solve Systems Of Linear Inequalities By Graphing Algebra 1 Practice

Which System Of Linear Inequalities Is Shown In The Graph The Graph Is Attached Y X 4 Y 3x Brainly In

1

Graphing Linear Inequalities

Which Graph Shows The Solution To The System Of Linear Inequalities 2x 3y 12 Y Lt 3 Brainly Com

Graph Graph Inequalities With Step By Step Math Problem Solver

1

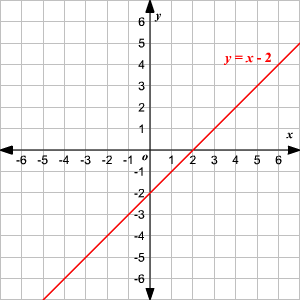
Graphing Systems Of Linear Inequalities

Solve And Graph 2x 3 9 2x 3 X X 3 Ppt Download

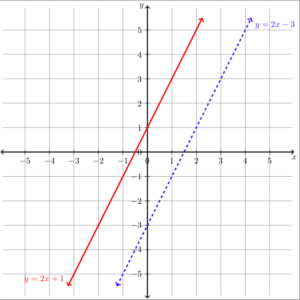
Graphs And Solutions To Systems Of Linear Equations Beginning Algebra

Search Q Graphing Inequalities On A Number Line Tbm Isch

System Of Linear Inequalities

Graphing Linear Inequalities Explanation Examples

Which Graph Represents The Solution Set Of The System Of Inequalities X Y Lt 12 Y X 4 Brainly Com

Graph Graph Equations With Step By Step Math Problem Solver

Solving And Graphing Linear Inequalities In Two Variables

Linear Inequalities How To Graph The Equation Of A Linear Inequality

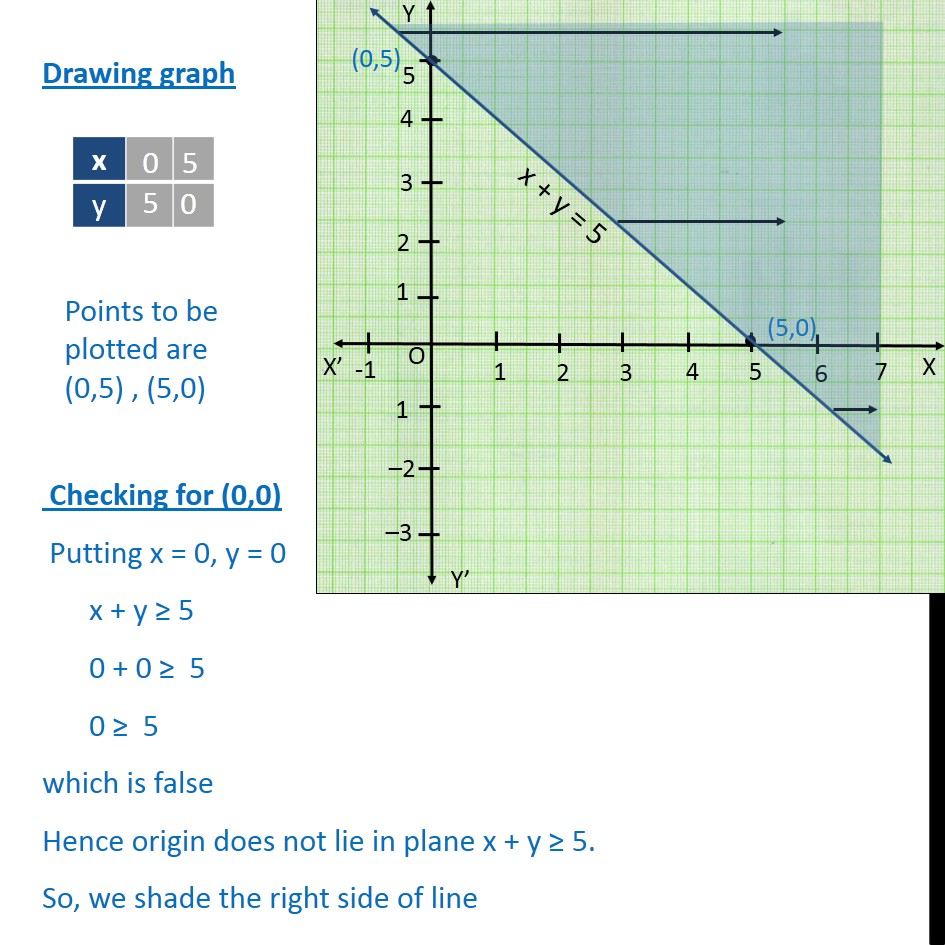
Example 12 Solve X Y 5 X Y 3 Graphically Examples

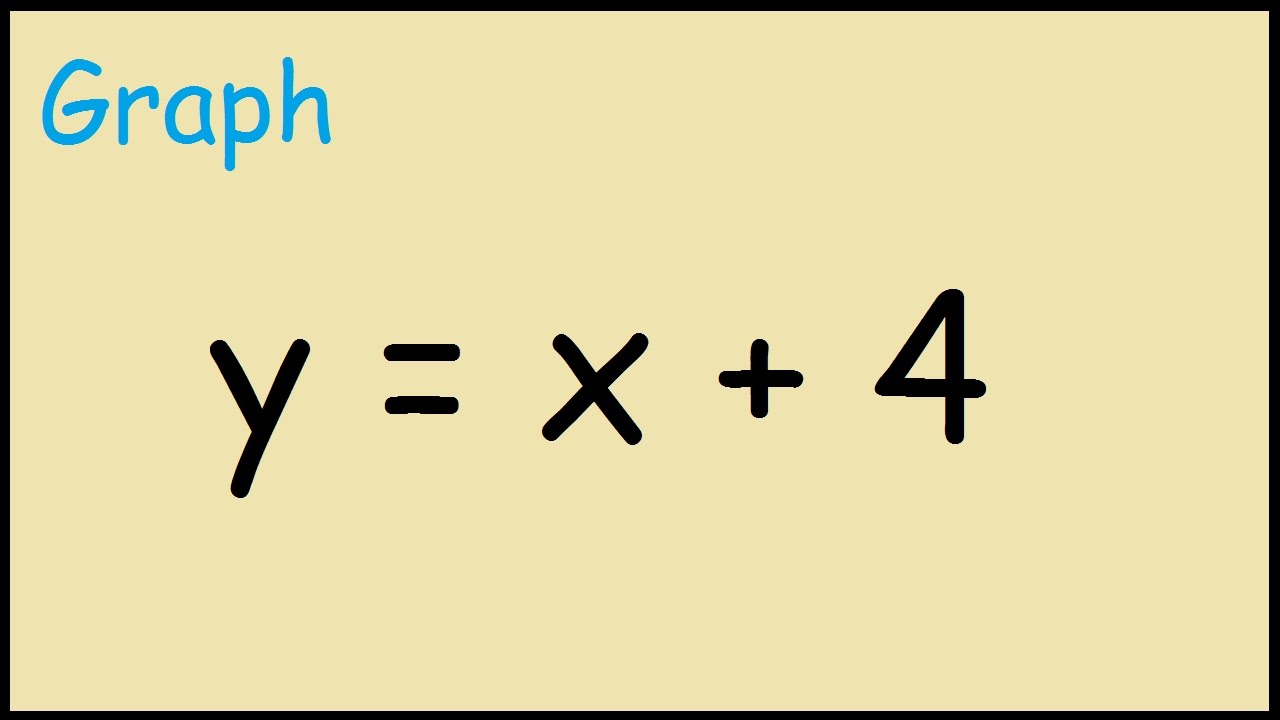
How To Graph Y X 4 Youtube

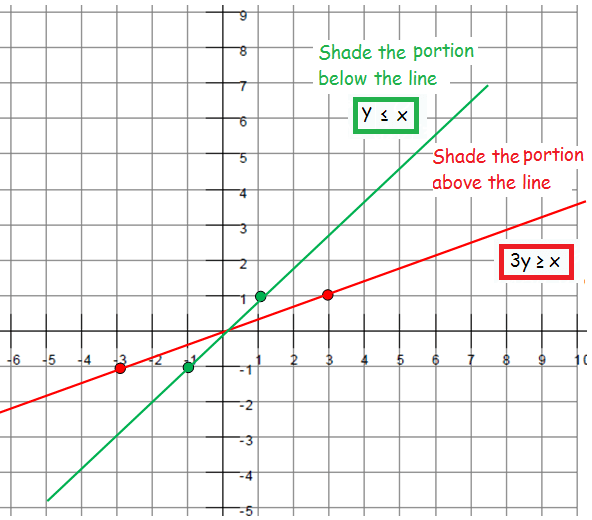
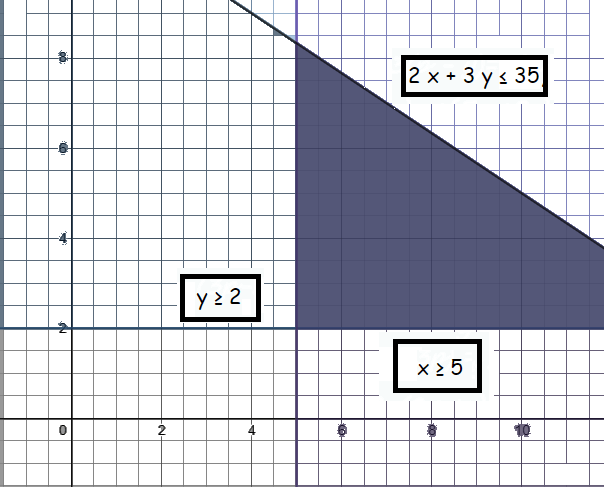
Graphing Linear Inequalities In Two Variables And Find Common Region

6 4 Linear Inequalities And Systems Of Linear Inequalities In Two Variables Hunter College Math101

Inequalities Graphing Inequalities Sparknotes

Consider This System Of Inequalities X Y Lt 3 The Lt Has A Line Under It Y Lt X 2 Brainly Com

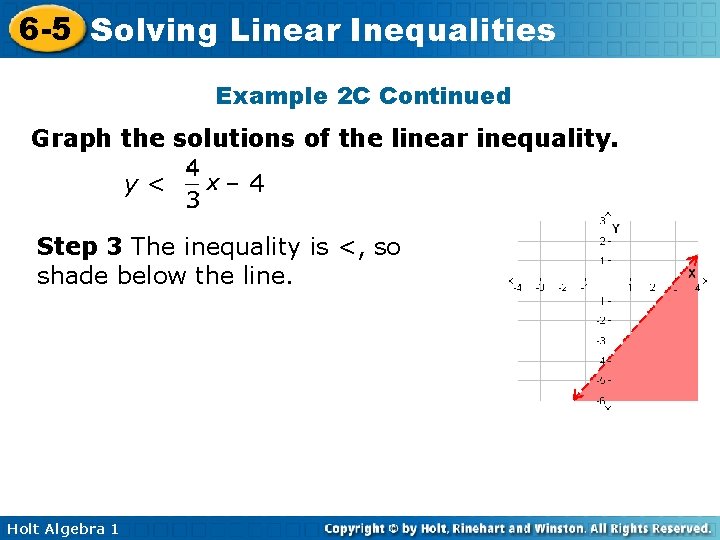
6 5 Solving Linear Inequalities Objective Graph And

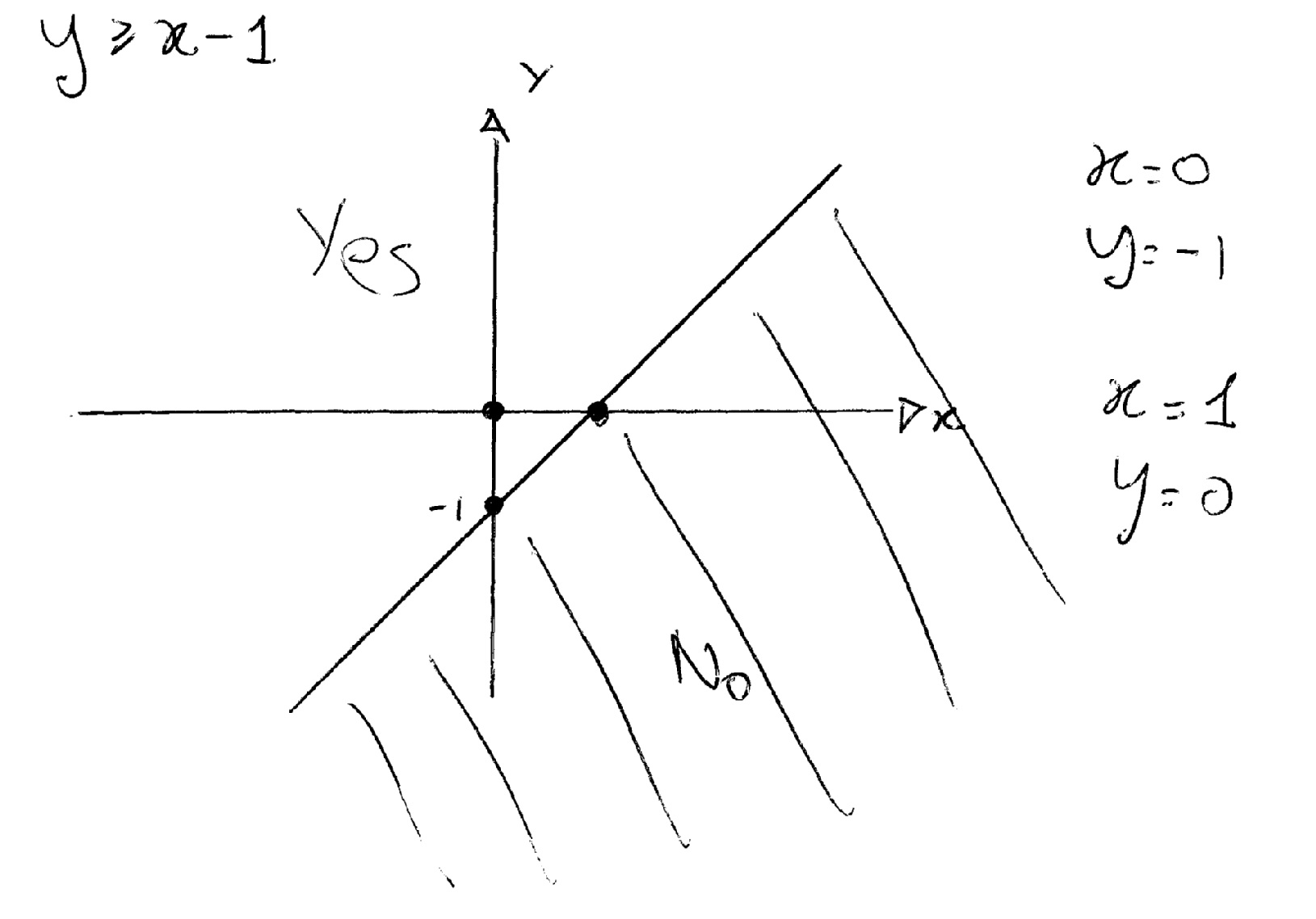
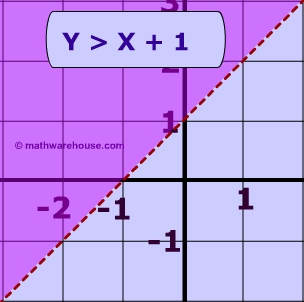
How Do You Graph The Inequality Y X 1 Socratic

Graphing Linear Inequalities

Linear Inequalities In Two Variables Ck 12 Foundation

Inequality Y 3x 4 Graph Novocom Top

Graphing Linear Inequalities

Solving And Graphing Linear Inequalities In Two Variables

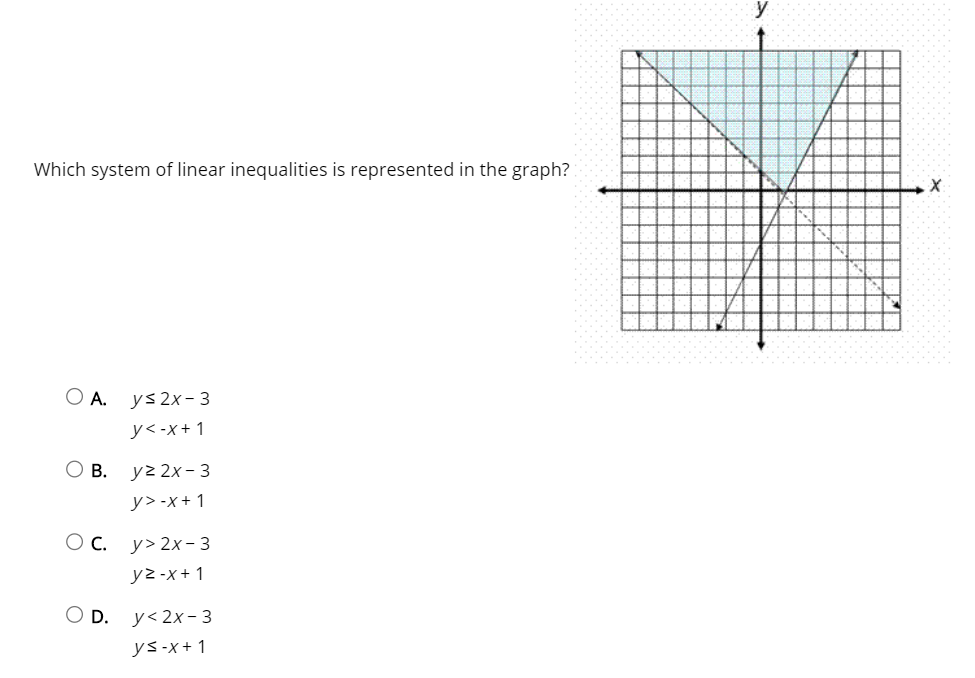
Y Which System Of Linear Equations Is Represented In Chegg Com

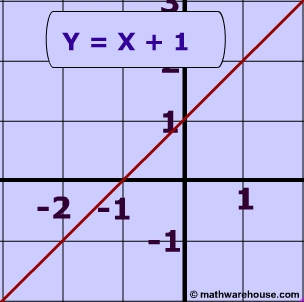
Linear Inequalities How To Graph The Equation Of A Linear Inequality

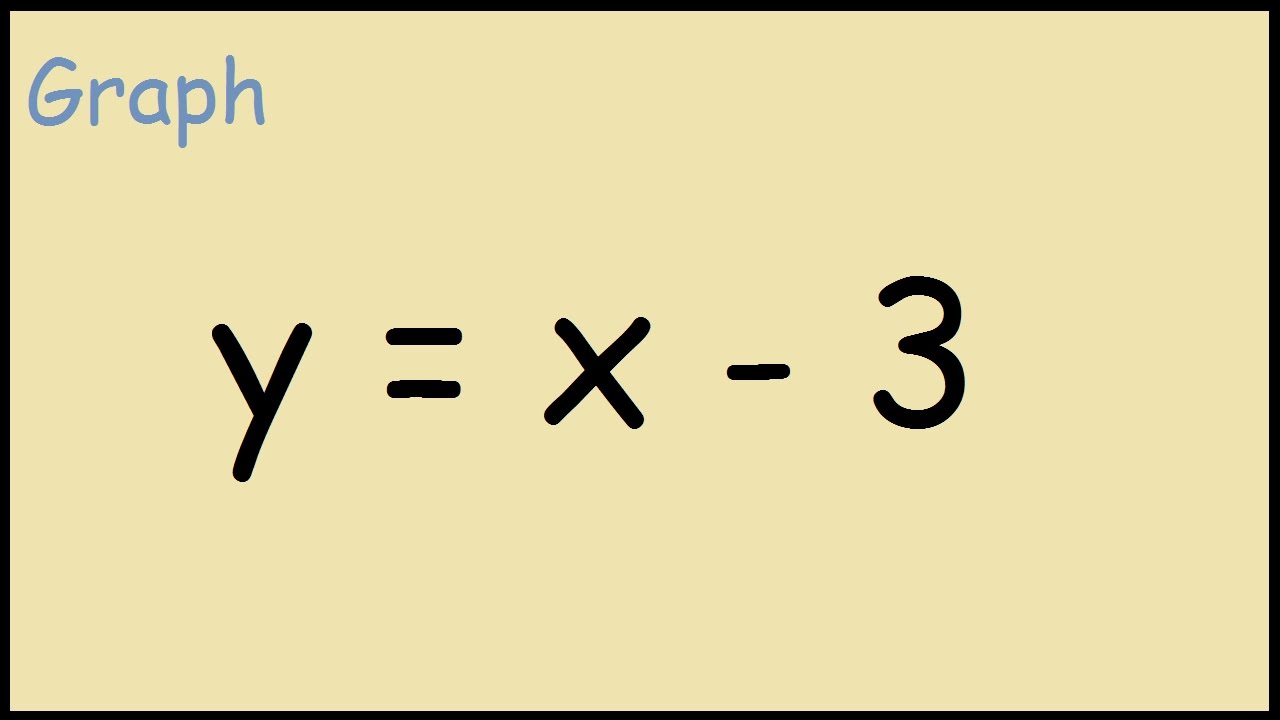
How To Graph Y X 3 Youtube

Incoming Term: y x-3 graph linear inequalities, how do you graph a linear inequality,